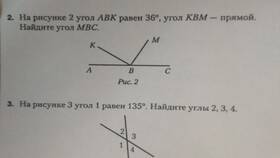
Сумма соседних углов - это важное понятие в геометрии, которое описывает взаимосвязь между углами, имеющими общую сторону и вершину. Рассмотрим основные свойства и примеры таких углов.
Содержание
Определение соседних углов
Соседние углы - это два угла, которые:
- Имеют общую вершину
- Имеют общую сторону
- Другие стороны этих углов лежат по разные стороны от общей стороны
Основное свойство соседних углов
Сумма соседних углов всегда равна 180°. Это свойство можно выразить формулой:
∠AOB + ∠BOC = 180°
где точка O - общая вершина, OB - общая сторона.
Примеры соседних углов
| Первый угол | Второй угол | Сумма |
| 45° | 135° | 180° |
| 90° | 90° | 180° |
| 120° | 60° | 180° |
Геометрические фигуры с соседними углами
Прямая линия
Когда два угла образуют развернутый угол (180°), они являются соседними.
Треугольник
В треугольнике внешний угол равен сумме двух внутренних углов, не смежных с ним.
Параллельные прямые и секущая
При пересечении параллельных прямых секущей образуются соседние углы, сумма которых равна 180°.
Доказательство свойства соседних углов
- Рассмотрим два соседних угла ∠AOB и ∠BOC
- Они вместе образуют развернутый угол ∠AOC
- Мера развернутого угла всегда равна 180°
- Следовательно, ∠AOB + ∠BOC = 180°
Применение свойства соседних углов
- Решение геометрических задач
- Доказательство теорем
- Построение чертежей
- Вычисление неизвестных углов
Важные следствия
Если один из соседних углов прямой
Если один угол равен 90°, то и второй тоже будет равен 90°.
Если углы равны
Если соседние углы равны между собой, то каждый из них равен 90°.
Связь с вертикальными углами
Сумма всех четырех углов, образованных двумя пересекающимися прямыми, равна 360°.
Практические задачи
| Условие | Решение |
| Один из соседних углов равен 75° | Второй угол: 180° - 75° = 105° |
| Соседние углы относятся как 2:3 | Углы равны 72° и 108° |
Ошибки и заблуждения
Важно не путать соседние углы с:
- Вертикальными углами (они равны, а не дают в сумме 180°)
- Накрест лежащими углами (при параллельных прямых они равны)
- Односторонними углами (их сумма также 180°, но определение другое)
Историческая справка
Свойства соседних углов были известны еще древнегреческим математикам. Евклид в своих "Началах" использовал эти свойства при доказательстве многих теорем.
Вывод
Сумма соседних углов всегда равна 180°. Это фундаментальное свойство широко применяется в геометрии и помогает решать разнообразные задачи. Понимание этой взаимосвязи углов является базовым для дальнейшего изучения геометрии.